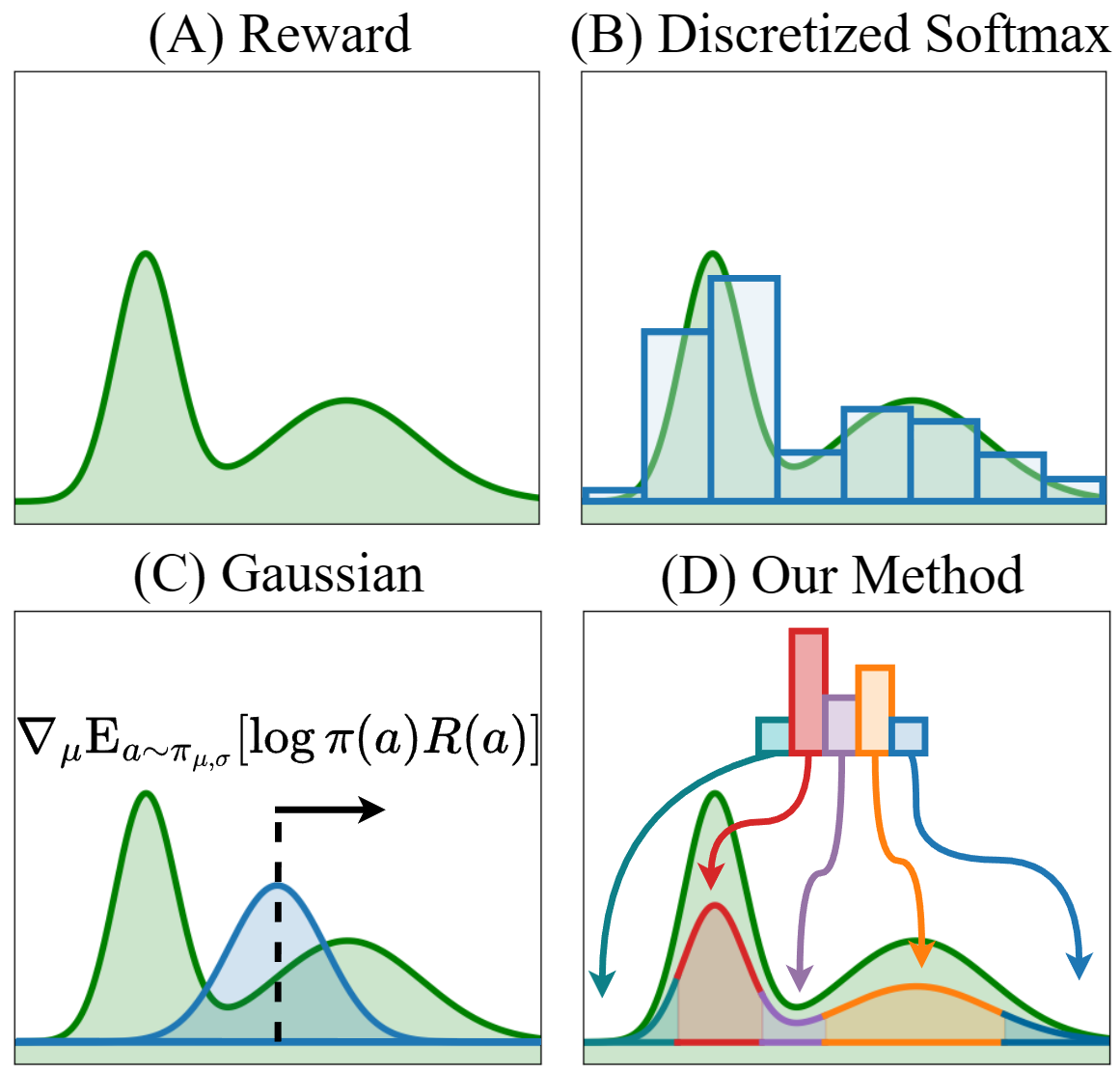
Consider maximizing a continuous reward function with two modalities as shown in (A). When the action space is properly discretized, a SoftMax policy can model the multimodal distribution and find the global optimum (B). However, discretization can lead to a loss of accuracy and efficiency. If we instead use a Gaussian policy by the common practice in literature, we will have trouble -- as shown in (C), even if its standard deviation is large enough to cover both modes, the policy gradient is pointing towards the local optimum. To address the issue, a more flexible policy parameterization is needed for continuous RL problems, one that is simple to sample and optimize.
This illustrative example compares the performance of our method with a single modality Gaussian policy optimized by REINFORCE. The Gaussian policy, initialized at 0 with a large standard deviation, can cover the whole solution space. However, the gradient is positive, which means the action probability density will be pushed towards the right, as the expected return on the right side is larger than the left side. As a result, the policy get stuck at the local optimum. In contrast, under the entropy maximization formulation, our method maximizes the reward while providing more chances for the policy to explore the whole solution space. Furthermore, our method can build a multimodal action distribution that fits the multimodal rewards, explore both modalities simultaneously, and eventually stabilize at the global optimum. This experiment suggests that a multimodal policy is necessary for reward maximization, and our method can help the policy better handle local optima.
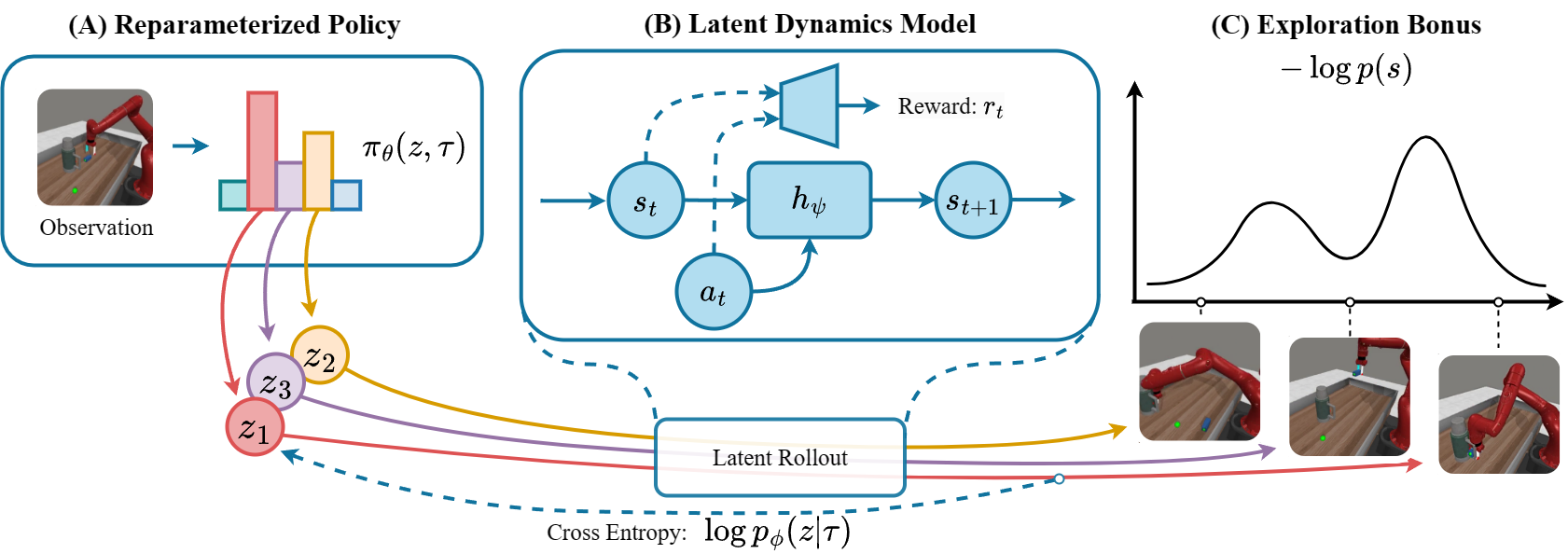
An overview of our model pipeline: A) a reparameterized policy from which we can sample latent variable z and action a given the latent state s; B) a latent dynamics model which can be used to forward simulate the dynamic process when a sequence of actions is known. C) an exploration bonus provided by a density estimator. Our Reparameterized Policy Gradient do multimodal exploration with the help of the latent world model and the exploration bonus.
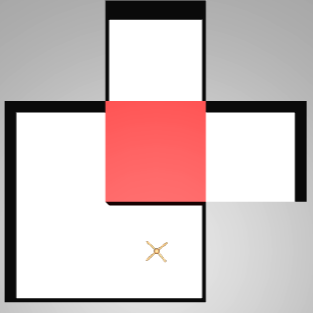
We apply RPG and single-modality model-based SAC on a 2D maze navigation task to maximize only the intrinsic reward (RND). The results suggests that our method explores the domain much faster, quickly reaching most grids, while the Gaussian agent (SAC) only covers the right part of the maze within a limited sample budget.





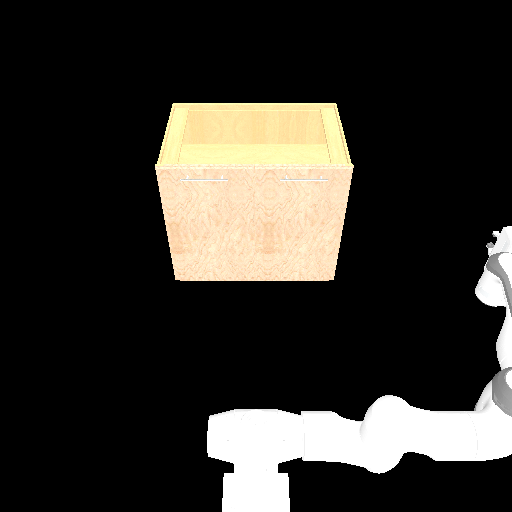

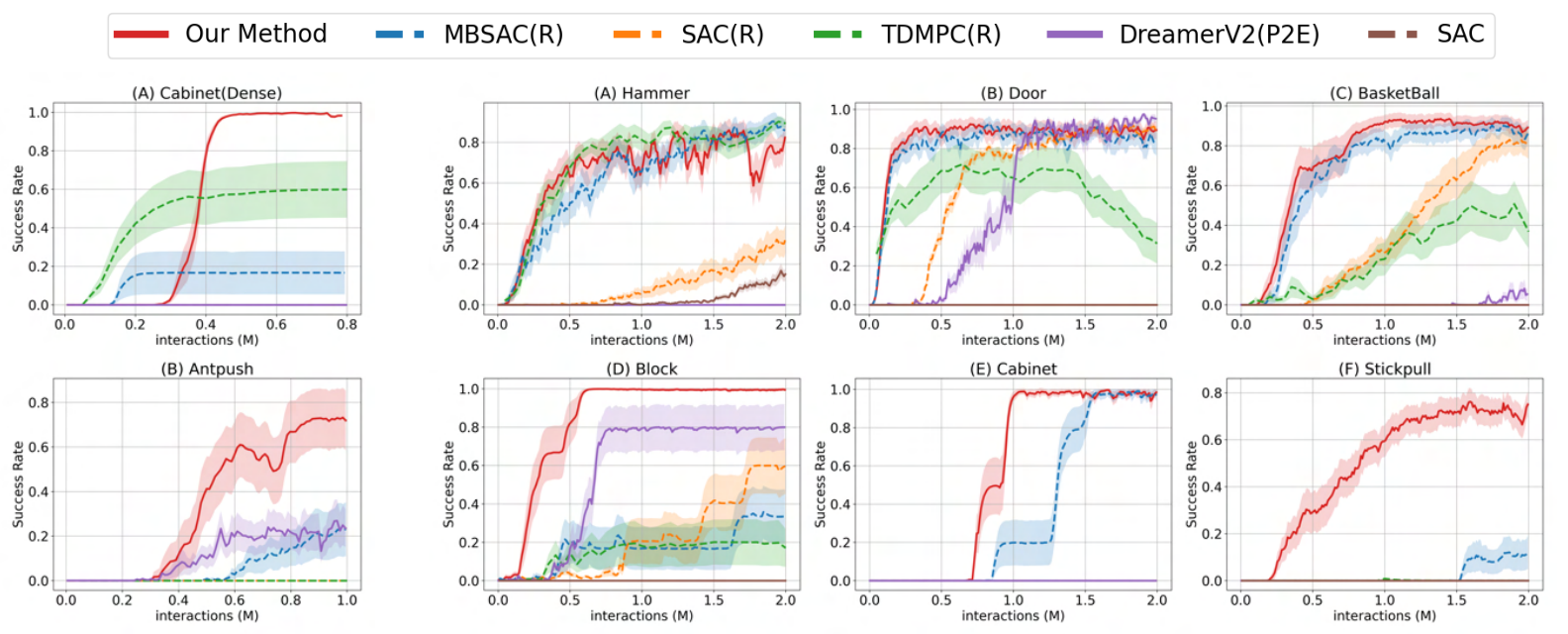
For dense reward tasks, our method largely improves the success rate on tasks with local optima. We can see that in both AntPush and Cabinet (Dense) tasks, our method outperforms all baselines. Our method consistently finds solutions, regardless of the local optima in the environments. For example, in the task of opening the cabinets' two doors and going to the two sides of the block, our method usually explores the two directions simultaneously and converges at the global optima. In contrast, other methods' performance highly depends on their initialization. If the algorithm starts by opening the wrong doors or pushing the block in the wrong direction, it will not escape from the local optima; thus, its success rates are low.
Our methods successfully solve the 6 sparse reward tasks. Especially, it consistently outperforms the MBSAC(R) baseline, which is a method that only differs from ours by the existence of latent variables to parameterize the policy. Our method reliably discovers solutions in environments that are extremely challenging for other methods (e.g., the StickPull environment), clearly demonstrating the advantages of our method in exploration. Notably, we find that MBSAC(R), which is equipped with our object-centric RND, is a strong baseline that can solve AdroitHammer and AdriotDoor faster than DreamerV2(P2E), proving the effectiveness of our intrinsic reward design. TDMPC(R) has a comparable performance with MBSAC(R) on several environments. We validate that it has a faster exploration speed in Adroit Environments thanks to latent planning. We find that the Dreamer(P2E) does not perform well except for the Block environment without the object prior and is unable to explore the state space well.
@article{huang2023reparameterized,
author = {Huang, Zhiao and Liang, Litian and Ling, Zhan and Li, Xuanlin and Gan, Chuang and Su, Hao},
title = {Reparameterized Policy Learning for Multimodal Trajectory Optimization},
journal = {ICML},
year = {2023},
}