Agenda

Agent-Environment Interface

• Agent: learner and decision maker.
• Environment: the thing agent interacts with, comprising everything outside the agent.
• Action: how agent interacts with the environment.
• In engineers’ terms, they are called controller, controlled system (or plant), and control signal.

Probabilistic Description of Environment: Markov Decision Processes

• A Markov decision process (MDP) is a Markov process with rewards and decisions.
• Definition:
• A Markov decision process is a tuple $(\mc{S}, \mc{A}, \mc{P}, \mc{R})$
  • $\mc{S}$ is a set of states (discrete or continuous)
  • $\mc{A}$ is a set of actions (discrete or continuous)
  • $\mc{P}$ is a state transition probability function
    • $\mc{P}^{a}_{s,s'}=P(s'|s,a)=\text{Pr}(S_{t+1}=s'|S_t=s,A_t=a)$
  • $\mc{R}$ is a reward function
    • $\mc{R}^{a}_{s}=R(s,a)=\bb{E}[R_{t+1}|S_t=s,A_t=a]$
  • Sometimes, an MDP also includes an initial state distribution $\mu$

Policy

• A policy is the agent's behaviour
• It is a map from state to action, e.g.,
  • Deterministic policy: $a=\pi(s)$
  • Stochastic policy: $\pi(a|s)=\text{Pr}(A_t=a|S_t=s)$

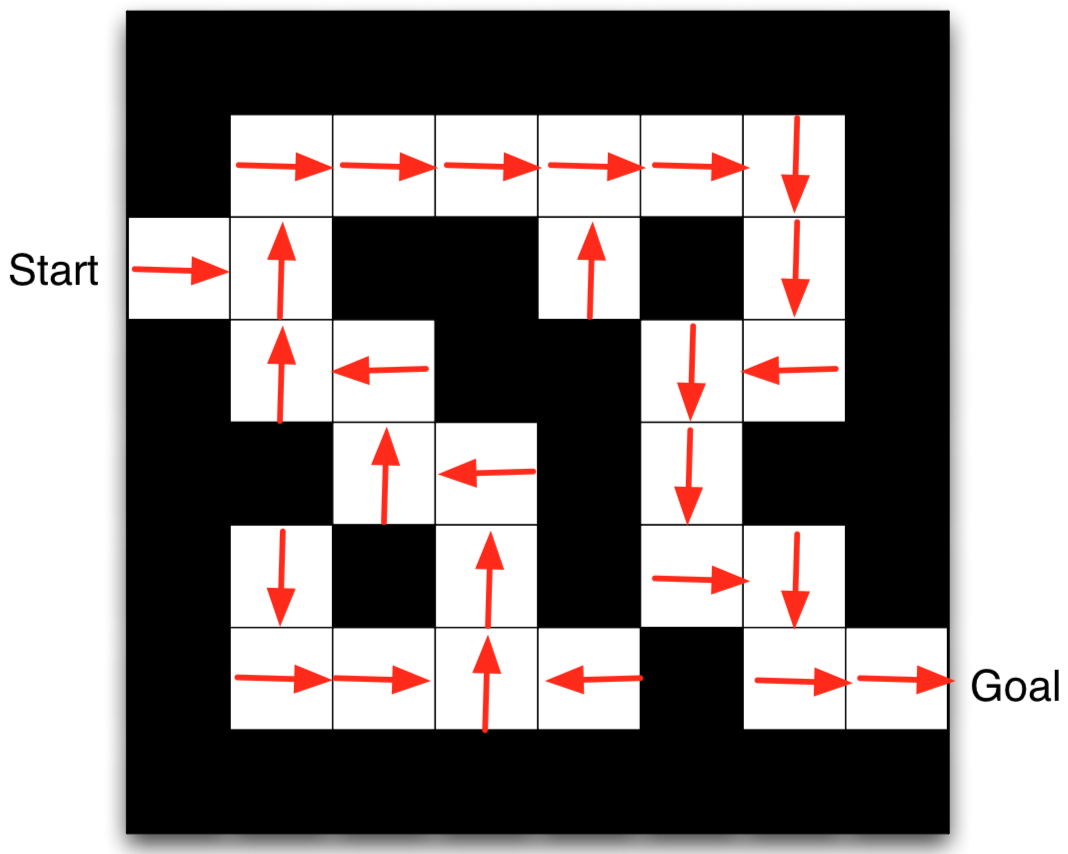
Maze Example: Policy

• Arrows represent policy $\pi(s)$ for each state s
• This is the optimal policy for this Maze MDP

Value Function

• Value function is a prediction of future reward
• Evaluates the goodness/badness of states
• State-value function
  • The state-value function $V_\pi(s)$ of an MDP is the expected return starting from state $s$, following the policy $\pi$
  • $V_\pi(s)=\bb{E}_\pi[G_t|S_t=s]$ (assuming infinite horizon here)
• Action-value function
  • The action-value function $Q_\pi(s,a)$ is the expected return starting from state $s$, taking action $a$, following policy $\pi$
  • $Q_\pi(s,a)=\bb{E}_\pi[G_t|S_t=s, A_t=a]$ (assuming infinite horizon here)
• Notation explanation:
  • In this lecture, when we write $\bb{E}_\pi$, it means we take expectation over all samples/trajectories generated by running the policy $\pi$ in the environment
  • So it counts for all the randomness from policy, initial state, state transition, and reward.

Maze Example: Value Function

• Numbers represent value $V_\pi(s)$ of each state $s$
• This is the value function corresponds to the optimal policy we showed previously

Optimal Value Function

• Due to the Markovian property, the return starting from a state $s$ is independent of its history. Therefore, we can compare the return of all policies starting from $s$ and find the optimal one.
• The optimal state-value function $V^*(s)$ is the maximum value function over all policies
  • $V^*(s)=\max_\pi V_\pi(s)$
• The optimal action-value function $Q_*(s,a)$ is the maximum action-value function over all policies
  • $Q^*(s,a)=\max_\pi Q_\pi(s,a)$
• The optimal value function specifies the best possible performance in the MDP.

Optimal Policy

• Define a partial ordering over policies \[ \pi\ge\pi'\mbox{ if }V_\pi(s)\ge V_{\pi'}(s), \forall s \]

Theorem: For any Markov Decision Process

• There exists an optimal policy $\pi_*$ that is better than, or equal to, all other policies, $\pi_*\ge\pi,~\forall\pi$
• All optimal policies achieve the optimal value function, $V_{\pi^*}(s)=V^*(s)$
• All optimal policies achieve the optimal action-value function, $Q_{\pi^*}(s,a)=Q^*(s,a)$

• An optimal policy can be found by maximizing over $Q^*(s,a)$, \[ \pi^*(a|s)= \begin{cases} 1, & \text{if}~~a=\text{argmax}_{a\in\mc{A}}~Q^*(s,a) \\ 0, & \text{otherwise} \end{cases} \]

Bellman Optimality Equation

• Optimal value functions also satisfy recursive relationships \[ \begin{aligned} V^*(s) & = \max_a Q^*(s,a) \\ & = \max_a\bb{E}_{\pi_*}[G_t|S_t=s, A_t=a] \\ & = \max_a\bb{E}_{\pi_*}[R_{t+1}+\gamma G_{t+1}|S_t=s, A_t=a] \\ & = \max_a\bb{E}[R_{t+1}+\gamma V^*(S_{t+1})|S_t=s, A_t=a] \\ \end{aligned} \]
• Similarly, for action-value function, we have
\[ Q^*(s,a)=\bb{E}[R_{t+1}+\gamma \max_{a'}Q^*(S_{t+1}, a')|S_t=s, A_t=a] \]
• They are called Bellman Optimality Equations

Solving the Bellman Optimality Equation

• Bellman Optimality Equation is non-linear (because there is the max operation).
• No closed form solution (in general)
• Many iterative solution methods:
  • Value Iteration
  • Policy Iteration
  • Q-learning (we will talk about this later)
  • SARSA

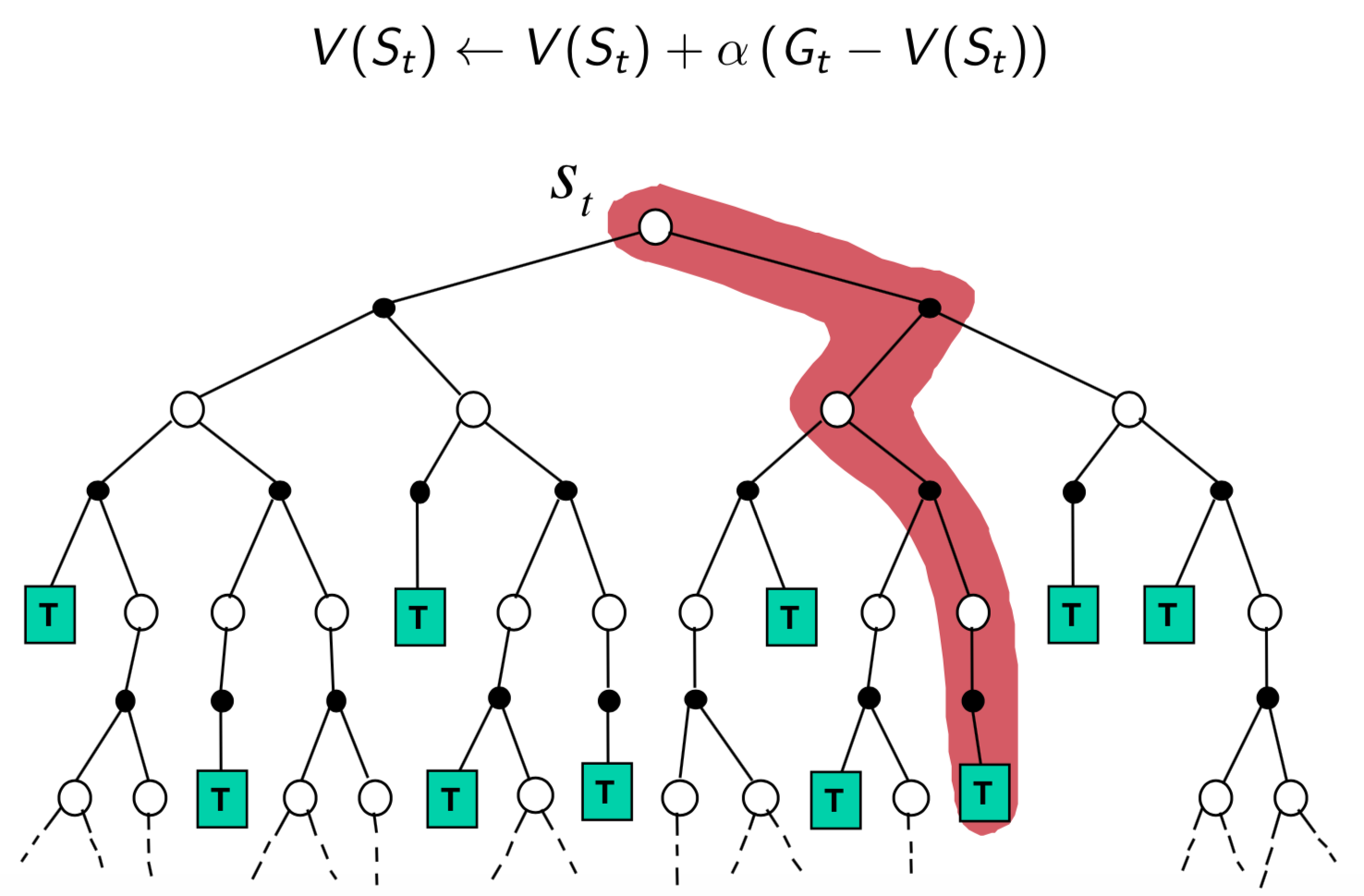
Monte-Carlo Policy Evaluation

• Basic idea: MC uses the simplest possible idea: value = mean return

• Learn $V_\pi$ from $K$ episodes under policy $\pi$
  • $\{S_{k,0}, A_{k,0}, R_{k,1}, ..., S_{k,T}\}_{k=1}^K\sim\pi$
• Recall that the return is the total discounted reward:
  • $G_t=R_{t+1}+\gamma R_{t+2}+...+\gamma^{T-t-1}R_T$
• Recall that the value function is the expected return:
  • $V_\pi(s)=\bb{E}_\pi[G_t|S_t=s]$

Monte-Carlo Policy Evaluation

• Suppose that we have collected a number of trajectories. Monte-Carlo policy evaluation uses empirical mean return to approximate expected return
  • For each episode:
    • For each time step $t$:
      • Compute empirical return $G_t$ from the current state $s$
      • Increment total return $S(s) \leftarrow S(s) + G_t$
      • Increment state visit counter $N(s) \leftarrow N(s) + 1$
  • Value is estimated by mean return $V(s)=S(s)/N(s)$

Monte-Carlo Methods

• Quick facts:
  • MC is unbiased (average of the empirical return is the true return)
  • MC methods learn directly from episodes of experience
  • MC is model-free: no knowledge of MDP transitions / rewards
• Caveat: can only apply MC to episodic MDPs
  • All episodes must terminate

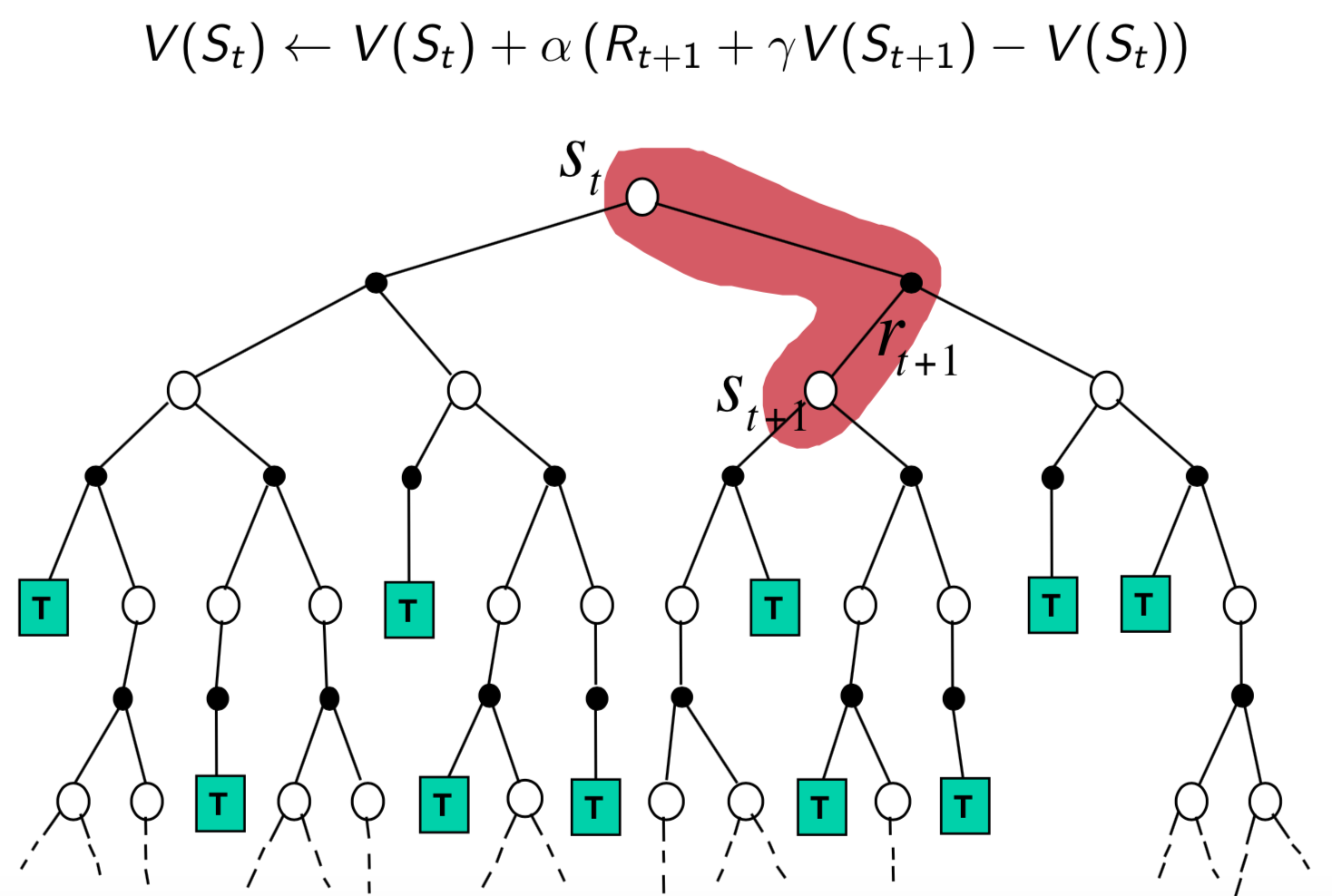
Temporal-Difference Learning

• Basic idea: TD leverages Bellman expectation equation to update the value function. \[ V_{\pi}(s)= \bb{E}_{\pi}[R_{t+1}+\gamma V_{\pi}(S_{t+1})|S_t=s] \]

Temporal-Difference Learning

• Learn $V_\pi$ from $K$ episodes under policy $\pi$
  • $\{S_{k,0}, A_{k,0}, R_{k,1}, ..., S_{k,T}\}_{k=1}^K\sim\pi$
• Simplest temporal-difference learning algorithm: TD(0)
  • Loop for a new iterations:
  • Sample $(S_t, A_t, R_{t+1}, S_{t+1})$ with replacement from the transitions in the episodes
  • Update value $V(S_t)$ toward estimated return $\color{red}{R_{t+1}+\gamma V(S_{t+1})}$:
  • $V(S_t) \leftarrow V(S_t) + \alpha(\color{red}{R_{t+1}+\gamma V(S_{t+1})}-V(S_t))$
  • $R_{t+1}+\gamma V(S_{t+1})$ is called the TD target
  • $\delta_t=R_{t+1}+\gamma V(S_{t+1})-V(S_t)$ is called the TD error
• If we expand one step further, we got TD(1)
  • $V(S_t) \leftarrow V(S_t) + \alpha(R_{t+1}+\gamma R_{t+2} + \gamma^2 V(S_{t+2})-V(S_t))$
  • Similarly, we can have TD(2), TD(3), ...

Temporal-Difference Learning

• Quick facts:
  • TD methods learn directly from episodes of experience
  • TD is model-free: no knowledge of MDP transitions / rewards
  • TD learns from incomplete episodes, by bootstrapping
  • TD updates a guess towards a guess

Key Differences between MC and TD

• MC estimates values based on rollout
• TD estimates values based on Bellman equation

Pros and Cons of MC vs. TD

• TD can learn before knowing the final outcome
  • MC must wait until the end of episodes
  • TD can learn online after every step

Pros and Cons of MC vs. TD

• TD can learn without the final outcome
  • MC can only learn from complete sequences
  • When some episodes are incomplete, TD can still learn
  • MC only works for episodic (terminating) environments
  • TD works in non-terminating environments

Bias/Variance Trade-Off

• Return $G_t=R_{t+1}+\gamma R_{t+2}+...+\gamma^{T-t-1}R_T$ is always an unbiased estimate of $V_\pi(S_t)$
• The true TD target $R_{t+1}+\gamma V_\pi(S_{t+1})$ is an unbiased estimate of $V_\pi(S_t)$
• If we will update $\pi$ slowly along the learning process,
  • the TD target $R_{t+1}+\gamma V(S_{t+1})$ becomes a biased estimate of $V_\pi(S_t)$, because
    • $V(S_{t+1})$ is a return estimation from the previous $\pi$.
  • However, the TD target also has much lower variance than the return $G_t$, because
    • the return $G_t$ is from a single rollout, heavily affected by the randomness (actions, transitions, and rewards) in all the future steps;
    • whereas the TD target is affected by the randomness in the next one step, and the low variance of the $V(S_{t+1})$ estimation from many historical rollouts.

Pros and Cons of MC vs TD (2)

• MC has high variance, zero bias
  • Good convergence properties (even with function approximation)
  • Independent of the initial value of $V$
  • Very simple to understand and use
• TD has low variance, some bias
  • Usually more efficient than MC
  • TD(0) converges to $V_\pi(s)$ (but not always with function approximation)
  • Has certain dependency on the initial value of $V$

Bellman, or no Bellman, that is the question

• Monte-Carlo sampling and Bellman equation are two fundamental tools of value estimation for policies.
• Each has its pros and cons.
• Based on them, there are two families of model-free RL algorithms, both well developed. Some algorithms leverage both.
• Fundamentally, it is about the balance between bias and variance (sample complexity).

We start from REINFORCE and Deep Q-Learning

• Reason I:
  • REINFORCE uses Monte-Carlo sampling
  • Deep Q-Learning (DQN) uses Bellman equation
• Reason II:
• REINFORCE only has a policy network
• DQN only has a value network

Taxonomy of RL Algorithms and Examples

The Anatomy of an RL algorithm

• Suppose we are going to learn the Q-function. Let us follow the previous flow chart and answer three questions:
1. Given transitions $\{(s,a,s',r)\}$ from some trajectories, how to update the current Q-function?
   • By Temporal Difference learning, the update target for $Q(S,A)$ is
     • $R+\gamma\max_a Q(S', a)$
   • Take a small step towards the target
     • $Q(S,A)\leftarrow Q(S,A)+\alpha[R+\gamma\max_a Q(S', a)-Q(S,A)]$
2. Given $Q$, how to improve policy?
   • Take the greedy policy based on the current $Q$
     • $\pi(s)=\text{argmax}_a Q(s,a)$
3. Given $\pi$, how to generate trajectories?
   • Simply run the greedy policy in the environment.
   • Any issues?

Failure Example

• Initialize Q
  • $Q(s_0,a_1)=0,Q(s_0,a_2)=0$
  • $\pi(s_0)=a_1$
• Iteration 1: take $a_1$ and update $Q$
  • $Q(s_0,a_1)=1,Q(s_0,a_2)=0$
  • $\pi(s_0)=a_1$
• Iteration 2: take $a_1$ and update $Q$
  • $Q(s_0,a_1)=1,Q(s_0,a_2)=0$
  • $\pi(s_0)=a_1$
• ...
• $Q$ stops to improve because the agent is too greedy!

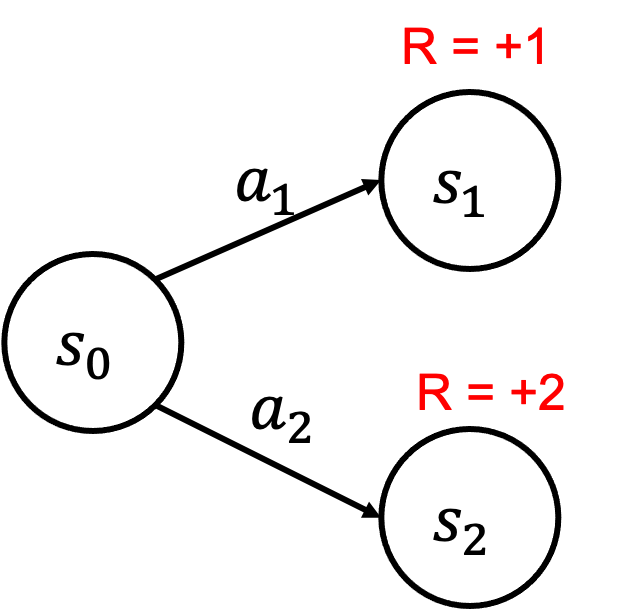
$\epsilon$-Greedy Exploration

• The simplest and most effective idea for ensuring continual exploration
• With probability $1-\epsilon$ choose the greedy action
• With probability $\epsilon$ choose an action at random
• All $m$ actions should be tried with non-zero probability
• Formally, \[ \pi_{\epsilon-Greedy}(a|s)= \begin{cases} \epsilon/m + 1-\epsilon, & \text{if}~~a=\text{argmax}_{a\in\mc{A}}~Q(s,a) \\ \epsilon/m, & \text{otherwise} \end{cases} \]

Exploration vs Exploitation

• Exploration
  • finds more information about the environment
  • may waste some time
• Exploitation
  • exploits known information to maximize reward
  • may miss potential better policy
• Balancing exploration and exploitation is a key problem of RL. We use will spend a lecture to discuss advanced exploration strategies.

Q-Learning Algorithm

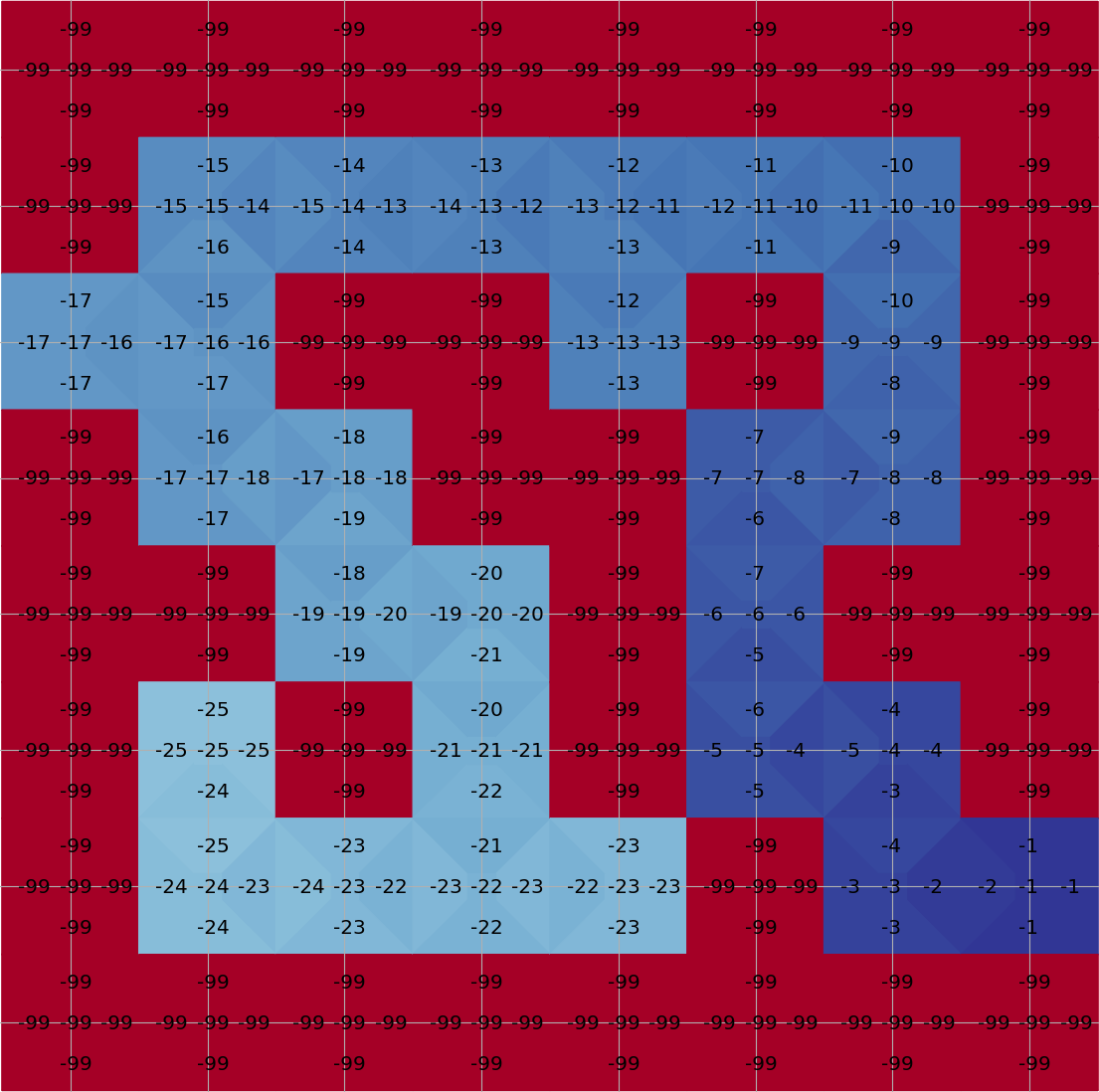
Running Q-learning on Maze